최소자승법 선형회귀 - 수식 유도, 장단점

일단 이걸 최소화시키는 세타를 찾아야 함
-> 미분해서 0되는 걸 찾자!

Wn에 대해 미분
각각에 대해 편미분하면??

위의 시그마 풀고 w1, w0에 대해 정리하면 이렇게 됨
이걸 이제 행렬에 적용할 필요가 있음

일단 각각 편미분한 거 0으로 넣고 간단히 정리하면 위와 같음

각각 X, w, y가 이렇게 있다고 치면
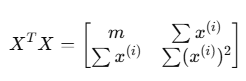
X를 트랜스포즈해서 곱할 시 이렇게 나옴
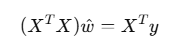
이 식을 풀어 계산하면 맨 처음 편미분한 식이랑 같게 나오고

가중치 w(세타)를 구하는 식을 유도 가능
수식 전개 과정

이렇게 표시 가능한데
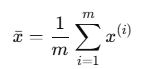
xˉ는 입력값들의 평균을 의미, 1/m 생겼으니 밖으로 m 나옴

행렬식(Determinant) 계산.. 역행렬을 구하기 위함
일단 대각선으로 엮어 곱해 빼고
m으로 묶고, 마지막으로 분산 공식
******************************************************************************************************
* 분산 공식

이건 평균인데
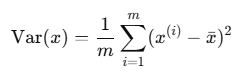
이게 분산

전개 시 이렇게 됨.. 근데 위에 나왔던 행렬식이랑 똑같음
******************************************************************************************************
이제 역행렬 구하기

* 역행렬 공식

이렇게 있으면

이때 ad - bc는 행렬식이고 0이 아니어야 행렬식이 존재

이제 대입하면 이렇게 정리됨

이건 그냥 단순 계산

행렬 풀고 정리하면 이렇게 변함
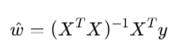
어쨌든 중요한 건 이거
w 개수랑 X 열 수랑 일치해야 하고, X 행 수랑 y개수랑 일치해야 함
장점
- 반복과 사용자가 지정하는 하이퍼 매개변수가 존재하지 않아 데이터만 있으면 쉽게 해 구하기 가능
단점
- 피쳐가 늘어나면 속도 느려짐(역행렬)
- 모든 데이터를 한 번에 처리 -> 메모리 사용량 급격히 늘어남
- 선형 회귀 모델에서만 사용 가능
다른 풀이
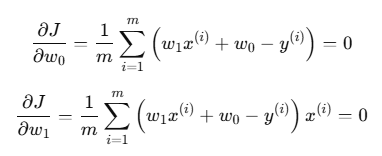
이게

각각 풀면 이렇게 됨

일단 다르게 접근하면, 이렇게 표기 가능한데(각각은 행렬)

벡터 내적 형태로 표현

이 성질을 활용

전개하면 이렇게 되는데, 이걸 미분하면?

여기서 y^Ty사라지고, 각각 미분하면

다시 정리하면

이걸 w에 대해 정리하면

이렇게 유도 됨
이 방식이 더 쉬운듯