| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 유니티
- unity
- Aegis
- gas
- ability task
- 언리얼 엔진
- linear regression
- 언리얼엔진
- animation
- 게임 개발
- gameplay ability system
- gameplay effect
- rpc
- photon fusion2
- MAC
- stride
- Unreal Engine
- C++
- listen server
- CTF
- gameplay tag
- 게임개발
- UI
- local prediction
- widget
- Multiplay
- 보안
- Replication
- attribute
- os
- Today
- Total
Replicated
형식 언어 본문
언어 (Language)
- 다른 개체들이 서로 의사소통을 하기 위한 도구
- Syntax (구문, 문법), Semantics (의미)
자연어 (Natual Lang.)
- 인간들끼리 소통하기 위해 사용되는 언어
- 자연적으로 만들어졌고, 규칙이 명확하지 않고 복잡함
- 해석이 다양할 수 있음
형식 언어 (Fornal Lang.)
- 누군가에 의해 특수한 목적을 위해 만들어진 언어
- 규칙이 단순, 명확
- 복잡한 인간의 생각을 다 표현할 수는 없음
- 해석의 오해가 없음
- 컴퓨터가 최종적으로 이해 가능
- 타입 0, 1, 2, 3
언어(Language): 알파벳으로부터 생성되는 모든 문자열들의 부분 집합
문법(Grammar): 언어는 문법에 의해 생성되고 정의됨
인식기(automata): 언어는 인식기에 의해 인식됨
언어와 인식기
| 문법 | 언어 | 인식기 |
| 타입 0 (무제약 문법) | 재귀 열거 언어 | 튜링 기계(turing machine) |
| 타입 1 (문맥인식 문법) | 문맥인식 언어 | 선형한계 오토마타 (linear-bounded automata) |
| 타입 2 (문맥자유 문법) | 문맥자유 언어 | 푸시다운 오토마타 (push-down automata) |
| 타입 3 (정규 문법) | 정규 언어 | 유한 오토마타 (finite automata) |
알파벳(Alphabet): 언어의 문장을 이루는 기본적인 기호(Symbol)
- 알파벳이란 공집합이 아닌 기호들의 유한 집합으로, Σ로 표시
- ex. Σ1 = {ㄱ, ㄴ, ㄷ, .. ㅎ} / Σ2 = {a, b, c .. z}
- 일반 프로그래밍 언어에서는 알파벳의 의미를 사용 가능한 문자나 기호들의 집합이라 설명
- C언어의 경우, 알파벳은 영문 소문자, 대문자, 숫자 0~9, 특수문자 +, *, -, _, ..등
문자열(String): 알파벳 Σ에 대한 문자열은 알파벳에서 정의된 기호들을 나열한 유한 수열(finite sequence)
- ex. Σ = {a, b, c} 일때 a, ca, ccab 등이 문자열
- = 문장(sentence), 단어(word)
- 문자열의 대표 이름은 u, v, w, ... 로 나타냄
- 예를 들어 w = abaaa => abaaa라는 값을 갖는 문자열의 이름이 w
문자열의 길이(Length)
- 문자열을 이루는 기호의 개수
- 어떤 문자열 w의 길이는 |w|로 표시, w의 cardinality
문자열의 접속(Concatenation)
- 두 개의 문자열을 연결하여 새로운 문자열을 만드는 연산
- u·v 혹은 uv로 표시
공문자열(Empty string)
- ε로 표기
- 어떤 문자열 u, v에 대하여..
- uε = u = εu, uεv = uv
- λ로도 표시하고, 널 문자열이라고도 함.
- 문자열에서의 연산 중 접속 연산은 ε을 항등원으로 취함
- a^n은 a가 n개 연결된 문자열, a^0는 공문자열(ε)을 나타냄
w^R은 문자열 w의 역(reverse)으로 w를 이후는 요소들의 역순으로 얻어짐- ex. w = ccba- w^R - abcc
접두사(Prefix)- 문자열 w = uv 일때, u를 문자열 w의 접두사라 함- 진접두사 (Proper prefix): u ≠ ε 인 접두사 (공문자열 아닌 접두사)
접미사(Suffix)- 문자열 w = uv일 때 v를 문자열 w의 접미사라 함- 진접미사 (Proper suffix): v ≠ ε인 접미사 (공문자열 아닌 접미사)
Σ* (reflexive transitive closure, Kleene closure)
- 공문자열을 포함하는 알파벳 Σ에 대한 접속 연산에 의해 만들어질 수 있는 모든 문자열들의 집합
- Σ-스타(Σ 스타, 클리니 클로저)라고 읽음
Σ+ (transitive closure, positive closure) : Σ*에서 공문자열을 제외한 모든 문자열의 집합
- Σ-대거(Σ dagger, 포지티브 클로저)라고 읽고 Σ+ = Σ* - {ε}
언어 L
- 알파벳 Σ에 대해서 Σ*의 부분집합
- 유한 언어(finite lang) : 언어에 속하는 문자열의 수가 유한 개일 경우
- 무한 언어(infinite lang) : 언어에 속하는 문자열의 수가 무한 개일 경우
- 언어는 의미(semantic)의 개념은 포함하지 않음
- 언어란 단지 문자열의 집합, 형식 언어 이론은 문자열 집합의 속성에 관한 이론
언어에서의 연산
합집합
- L ∪ M -> L에 속하는 문자열이거나 M에 속하는 문자열
- L ∪ M = { s | s ∈ L or s ∈ M }
접속
- 두 언어 L과 M의 접속 LM은 L에 속하는 문자열과 M에 속하는 문자열을 접속한 것
- 교환 법칙 성립 안함
L의 거듭제곱
- 언어 L의 거듭제곱은 재귀적으로 다음과 같이 정의
- L^0 = {ε}
- L^n = LL^n-1
클리니 클로저, 포지티브 클로저
- 언어 L의 클리니 클로저 L*은 다음과 같이 정의
- L* = L^0 ∪ L^1 ∪ .... =
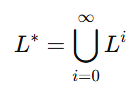
- 포지티브 클로저 L+는
- L+ = L^1 ∪ L^2 ∪ .... =

- L+ = L* - L^0
'학부 > 오토마타와 컴파일러' 카테고리의 다른 글
| 유한 오토마타 - 상태전이도 & 형식적 표현 (0) | 2025.10.10 |
|---|---|
| 문법의 표기법 2 (문법 도표, BNF, EBNF) (0) | 2025.10.10 |
| 문법의 표기법 1 (정규 표현) (0) | 2025.10.09 |
| 형식 문법 (0) | 2025.10.08 |
| 컴파일러 개론 (0) | 2025.10.04 |
