| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- os
- MAC
- Replication
- gameplay ability system
- 게임 개발
- unity
- Multiplay
- ability task
- listen server
- CTF
- UI
- gameplay tag
- C++
- stride
- 언리얼 엔진
- rpc
- Unreal Engine
- 유니티
- local prediction
- Aegis
- 언리얼엔진
- 보안
- photon fusion2
- gas
- 게임개발
- gameplay effect
- animation
- attribute
- linear regression
- widget
- Today
- Total
Replicated
신경망 학습 본문
활성 함수
- 여러 함수가 사용될 수 있으며 시그모이드가 대표적
시그모이드
import numpy as np
def SIGMOID(x):
return 1/(1 + np.exp(-x))- 가중합 v의 값을 0과 1 사이의 값으로 변환
- f(x) = 1 (1 + e^-x)
소프트맥스

import numpy as np
def SOFTMAX(x):
e_x = np.exp(x)
return e_x / e_x.sum(axis=0)- 시그모이드는 자신의 노드로 들어오는 신호의 가중합만 고려하여 출력 값 조절
- 소프트맥스 함수는 출력 노그가 여러 개일때 다른 노드로 들어오는 신호의 가중합도 고려
- 합이 1이라 각 출력에 대한 확률의 의미를 가짐
delta rule
- 신경망의 출력값과 정답 사이의 오차를 가지고 w를 조정하는 방법 중 하나
- 어떤 입력 노드가 출력 노드의 오차에 기여했다면 두 노드의 연결 가중치는 해당 입력 노드의 입력값과 오차에 비례하여 조절한다
- 역전파의 한가지 타입
- 비용함수가 MSE이면 경사하강법임
φ(v) = v 일때,
w←w+Δw
Δw = αex
wij <- wij + αejxi
이고 α=0.5 이면
x = [0.2, 0.9, 0.5]
w = [0.3, 0.4, 0.5]
φ(v) = 0.67, d = 1
e = 1 - 0.67 = 0.33
Δw = 0.5 * 0.33 * x = [0.033, 0.1485, 0.0825]
w = [0.333, 0.5485, 0.5825]
다시 계산 시,
e = 1 - 0.8515 = 0.1485
Learning rate
- 학습률, 0 < α <= 1
- α 값이 작으면 w의 변동폭이 작아짐, 학습 시간이 길어지는 대신 정답에 보다 근접할 수 있음. 또는 정답에 근접하기 전에 max iter limit에 걸려 학습이 멈출 수 있음
- α 값이 크면 w의 변동폭이 커짐, 학습시간이 짧아지는 대신 정답 부근에서 멈추어 접근이 안될 수 있음. 경우에 따라서는 정답에 수렴하지 않고 발산함
Generalize delta rule
w←w+Δw
Δw = αex
wij <- wij + αejxi
이 식은 활성함수가 φ(v) = v일때만 유효
4. w←w+Δw
3. Δw = αδx
2. δ = φ'(v)e
1. e = d - y
wij = wij + αφ'(v)exi
활성함수 미분한 거 넣으면 됨
φ(v) = v
-> φ'(v) = 1
φ(v) = 1 / (1 + e^-v)
-> φ'(v) = φ(v)(1 - φ(v))
즉, y(1-y)
delta
- 연결 가중치 값을 업데이트.. 목표는 업데이트된 w에 의해 산출되는 y와 d의 오차가 줄어들게 하는 것
- 경사하강법에 의해 오차가 줄어들도록 할 수 있음
- 경사하강법으로 W를 갱신하려면 손실 L을 W에 대해 미분한 값을 알아야 함
- 이것을 갱신하는 과정에서 활성 함수의 미분이 필요
- 기울기의 크기: W에 적용할 손실의 크기
- 기울기의 방향: 손실을 더할지 뺄지 여부 결정
wij = wij + αφ'(v)exi
- α : 반영할 에러의 크기를 조절
- φ'(v): 에러의 방향, 크기를 지정
- exi: w를 갱신할 값의 크기.
- e = d - y : 느린 학습 시간, 에러의 방향 있음
- e = (d - y)^2 : 빠른 학습 시간, 에러의 방향 없음
x = np.array([0.5,0.8,0.2])
w = np.array([0.4,0.7,0.8])
d = 1
alpha = 0.5
for i in range(50):
v = np.sum(w * x)
y = SIGMOID(v)
e = d - y
print("error",i,e)
w = w + alpha * y * (1-y) * e * x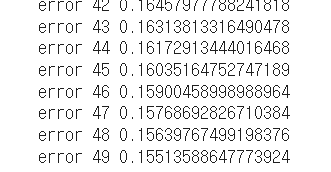
시그모이드 델타 룰 예시
Multi-output perceptron
뉴럴 네트워크 계산은 행렬로 표현됨
W12
-> 입력 층 1번 노드에서 출력층 2번으로 간다는 식의 표기 (표기법은 다양..)
v = W^Tx
a = np.array([[1,2,3],[4,5,6]])
b = np.array([[7,8],[9,10],[11,12]])
c = np.matmul(a,b)a 2*3
b 3*2
-> 2*2 행렬
One-hot encoding
클래스가 a, b, c 세 개?
1 0 0
0 1 0
0 0 1 이런 식으로 표현 가능
import numpy as np
target = np.array([0,1,2])
num = np.unique(target, axis=0)
num = num.shape[0]
encoding = np.eye(num)[target]
print( encoding )단위 행렬 만들고 그걸 이용해 원 핫 인코딩하는 코드
비용 함수(Cost function)
== 손실함수(Loss function)
- 에러를 측정하는 방법
- MSE, Cross entropy 많이 사용
MSE
- 예측값과 정답의 차를 제곱해서 다 더하고 평균낸 거
y = [0.2, 0.1, 0.3]
d = [0, 1, 0] 이면
MSE = ( 0.04 + 0.81 + 0.09 ) / 3 = 0.94 / 3 = 0.31
Cross Entropy
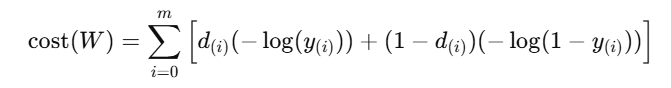
di가 1이면 오른쪽이, 0이면 왼쪽이 사라짐
로그라 예측에 가까울 수록 에러값이 작아짐
Sqaure Error 방식보다 더 에러에 민감함
가중치 갱신
- 데이터셋 전부 업데이트.. 오래 걸림
Stochastic 경사하강법 (SGD, stochastic gradient descent)
- 하나의 학습 데이터마다 오차를 계산하여 신경망의 가중치를 업데이트
배치(batch)
- 모든 학습 데이터의 오차에 관해 가중치 갱신값을 계산한 다음, 평균값으로 가중치를 한 번 업데이트
- 학습에 시간이 많이 걸림
미니 배치 (mini batch)
- SGD와 배치 방식의 중간
- 전체 학습 데이터에서 일부 데이터만 골라 배치 방식으로 학습
SGD 방식이 배치보다 오차가 빨리 줄어듬
미니 배치가 오차를 가장 많이 줄여줌
Epoch
- 전체 학습 데이터를 한번씩 모두 학습시킨 횟수(데이터셋 한 번 순회)
- 9개의 데이터를 세 부분으로 나누어 10회 학습 시킨 경우
-> 배치 사이즈는 3, 에폭은 10
'학부 > 딥러닝' 카테고리의 다른 글
| Keras 개요 (0) | 2025.10.18 |
|---|---|
| DNN (0) | 2025.10.18 |
| 인공신경망 개요 (0) | 2025.10.18 |
| Feature Selection, Model Stacking (0) | 2025.10.18 |
| Classification / 결정 트리, SVM, XGBoost (0) | 2025.10.13 |
