| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Aegis
- 언리얼엔진
- gameplay tag
- ability task
- unity
- 보안
- rpc
- gameplay effect
- Replication
- attribute
- stride
- os
- 유니티
- gas
- Multiplay
- widget
- linear regression
- animation
- UI
- C++
- listen server
- 게임개발
- MAC
- photon fusion2
- 게임 개발
- 언리얼 엔진
- local prediction
- gameplay ability system
- Unreal Engine
- CTF
- Today
- Total
Replicated
신경망 학습 / 수치미분 본문
데이터 주도 학습
손글씨 이미지를 보고 무슨 숫자인지 알아볼 수 있어야 함
이미지에서 특징(feture)를 추출한 후, 그 특정 패턴을 머신러닝 기술로 학습
- 컴퓨터 비전 분야에서는 SIFT, SURF, HOG 등(기계학습)의 특징을 많이 사용했음
- 하지만 이미지를 특징 벡터로 변환하는 로직은 여전히 사람이 설계
딥러닝 방식은 사람의 개입을 최소화 가능
- End-to-end 러닝 (종단 간 러닝): 데이터 입력부터 결과 출력까지 사람의 개입 없이 얻는다는 뜻
- 종단 간 러닝이 편리하지만 성능이 무조건 좋은 건 아님. 최근 딥러닝 알고리즘들은 피쳐 기반 방법을 적절히 섞어 사용
손실 함수
- 신경망 학습에서 사용하는 지표는 손실 함수(loss function)
- 기본 손실함수: 평균 제곱 오차, 교차 엔트로피 오차
- 적절한 손실 함수를 설계하는 것 자체가 연구가 될 수 있음
1. 평균 제곱 오차

- 오차 제곱합
- 여기서 yk 는 신경망의 출력(신경망이 추정한 값), tk는 정답 레이블, k는 데이터의 차원 수
- 손글씨 숫자 인식 예시에선 값이 0~9 이니 총 원소 10개짜리 데이터
- t: 한 원소만 1로 하고 그 외는 0으로 나타내는 표기법을 원-핫 인코딩 이라 함
import numpy as np
def mean_squared_error(y, t):
return 0.5 * np.sum( (y - t)**2 )
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
mse = mean_squared_error(np.array(y), np.array(t))
print(mse) # 0.0975
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
mse = mean_squared_error(np.array(y), np.array(t))
print(mse) # 0.5975예시
2. 교차 엔트로피(Cross Entropy) 오차

- 정답일 때의 자연 로그를 계산
- tk는 원-핫 인코딩
- 정답 클래스에 해당하는 자연로그를 계산하는 식이 됨
- ex. 정답레이블이 2일 때 2 클래스의 신경망 출력이 0.6 => -log0.6 = 0.51
- 정답에 해당하는 출력이 커질수록 0에 다가가고, 출력이 1일 때 0이 됨
- 반대로 반대로 정답일 때의 출력이 작아질 수록 오차가 커짐
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
cee = cross_entropy_error(np.array(y), np.array(t))
print(cee) # 0.510825457099
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
cee = cross_entropy_error(np.array(y), np.array(t))
print(cee) # 2.30258409299예시
정답 클래스가 2일 때 확률을 변경하여 크로스 엔트로피 오차가 변화함
미니배치 학습
- 기계학습 문제는 훈련 데이터에 대한 손실 함수의 값을 구하고, 그 값을 최대한 줄여주는 매개변수를 찾아냄
- 모든 훈련 데이터를 대상으로 손실 함수 값을 구해야 함 -> N으로 나눠 평균 손실 함수를 구함
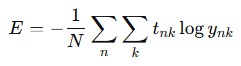
데이터가 N개라면 tnk는 n번째 데이터의 k번째 값을 의미
ynk는 신경망의 출력, tnk는 정답 레이블
* 왜 평균을 구하는가?
- 배치 돌릴 때 배치가 끝에 모자랄 수 있음. 그냥 쓰면 마지막 부분 로스가 엄청 작아질 것
- 신경망 학습에서도 훈련 데이터로부터 일부만 골라 학습 수행. 미니 배치 (mini-batch)
# 무작위 10개 추출
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
print(batch_mask)
print(t_batch)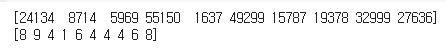
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t]+1e-7)) / batch_size배치용 교차 엔트로피
y[np.arange(batch_size), t] : 각 데이터의 정답 레이블에 해당하는 신경망의 출력을 추출
ex. 정답이 클래스 2 -> log(y[2])
정확도를 높이는 것이 목적인데 정확도 대신 손실함수를 지표로 쓰는 이유?
- 정확도는 매개변수의 미소한 변화에 거의 반응을 안하고, 반응을 해도 불연속적으로 갑자기 변화함. 계단함수와 유사한 문제
- 학습은 매개변수의 미분(기울기)을 계산하고 그 미분 값을 단서로 매개변수 값을 서서히 갱신하는 과정을 반복
- 계단 함수의 미분은 대부분의 장소에서 0, 매개변수의 작은 변화를 계단 함수가 말살하여 손실 함수 값에는 변화가 나타나지 않음
- 시그모이드 함수의 미분은 어느 장소라도 0이 되지는 않음
미분
- 한 순간의 변화량
- 직은 변화로 나누고, 그 변화를 한없이 0에 가깝게 함
def numerical_diff(f, x):
h = 1e-4
return (f(x + h) - f(x - h)) / (2 * h)- 중심 차분, 중앙 차분: 수치 미분의 오차를 줄이기 위해 x를 중심으로 전후의 차분을 계산
def function_1(x):
return 0.01*x**2 + 0.1*x이 함수를 미분한다고 하자
print(numerical_diff(function_1, 5))
print(numerical_diff(function_1, 10))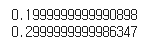
정답과 거의 유사한 값이 나옴
편미분
- 변수가 2개 이상인 식에 대해 각각의 변수로 미분
def function_2(x):
return x[0]**2 + x[1]**2# x0 = 3, x1 = 4일 때, x0에 대한 편미분을 구하라.
def function_tmp1(x0):
return x0**2 + 4.0**2.0
def function_tmp2(x1):
return 3.0**2.0 + x1 * x1
print(numerical_diff(function_tmp1, 3.0))
print(numerical_diff(function_tmp2, 4.0))
두 개의 편미분을 동시에 계산하고 싶다면?
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x) # x와 형상이 같은 배열을 생성
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h) 계산
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h) 계산
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 값 복원
return gradprint(numerical_gradient(function_2, np.array([3.0, 4.0])))
print(numerical_gradient(function_2, np.array([0.0, 2.0])))
print(numerical_gradient(function_2, np.array([3.0, 0.0])))
기울기의 의미
- 기울기 벡터의 반대 방향은 각 장소에서 함수의 출력값을 가장 크게 줄이는 방향
경사하강법
- 매개변수 공간이 광대하여 어디가 최소값이 되는 곳인지 짐작할 수가 없음
- 이런 상황에서 기울기를 잘 이용하여 함수의 최소값(혹은 가능한 한 작은 값)을 찾으려는 것이 경사하강법
# f:최적화하려는 함수
# init_x : 초깃값
# lr : 학습률
# step_num : 반복횟수
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append(x.copy())
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)init_x = np.array([-3.0, 4.0])
x, x_history = gradient_descent(function_2, init_x, lr= 0.07)
print(x)학습률을 조정하여 f(x0, x1) = x0^2 + x1^2 의 최소값 구하기


각 가중치 원소에 대한 편미분
1행 1번째 원소 -> w11을 조금 변경했을 때 손실함수 L이 얼마나 변화하느냐를 나타냄
손실함수 값이 감소하는 방향으로 학습
* 편미분 값이 음수값이면 w를 h만큼 변화시켰을 때 L이 감소된다는 의미, 따라서 w는 양의 방향으로 갱신됨
학습 알고리즘 구현
1. 미니배치
- 훈련 데이터 중 일부를 무작위로 가져오기
- 이렇게 선별한 데이터: 미니배치, 미니배치의 손실함수 값을 줄이는 것이 목표
2. 기울기 산출
- 미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기 구하기
- 기울기는 손실함수 값을 가장 작게 하는 방향을 제시
3. 매개변수 갱신
4. 1~3단계 반복
'학부 > 빅데이터마이닝' 카테고리의 다른 글
| 신경망 학습 관련 기술들 (0) | 2025.06.08 |
|---|---|
| 오차 역전파법 (Backward Propagation) (0) | 2025.06.08 |
| 신경망 손글씨 분류 (MNIST), 순전파(forward propagation) (0) | 2025.06.08 |
| 신경망 (0) | 2025.06.07 |
| 퍼셉트론 (Perceptron) (0) | 2025.06.07 |



