| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- rpc
- gameplay ability system
- gas
- linear regression
- photon fusion2
- widget
- 게임개발
- local prediction
- attribute
- animation
- Multiplay
- 보안
- ability task
- gameplay tag
- 언리얼엔진
- MAC
- unity
- 게임 개발
- gameplay effect
- Unreal Engine
- C++
- Aegis
- 언리얼 엔진
- os
- 유니티
- UI
- CTF
- Replication
- stride
- listen server
- Today
- Total
Replicated
오차 역전파법 (Backward Propagation) 본문
신경망 학습 과정
1. 순전파 (Forward Propagation)
2. 손실함수 계산
3. 역전파 (Backward Propagation)
4. 파라미터 업데이트
수치 미분 vs 오차 역전파법
수치미분
- 단순하고 구현하기 쉽지만 계산 시간이 오래 걸림. 파라미터 수가 많을수록 연산량 증가
- ex. 파라미터 100만개 -> 백만번 계산
- 딥러닝 모델은 많은 수의 파라미터를 가지므로 수치 미분으로는 실시간 학습 불가능
- 근사치여서 오차항에 민감
오차 역전파법
- 한 번의 순전파와 역전파로 모든 파라미터 기울기를 동시 계산
- 수학적으로 정확한 도함수 계산
계산 그래프
계산 과정을 표현한 그래프
- 국소적 계산을 전파함으로써 최종 결과를 얻음
- 4000 + 200 = 4200.. 4000이라는 숫자가 어떻게 계산되었느냐는 상관없이 단지 두 숫자를 더하면 됨
- 왼쪽 -> 오른쪽: 순전파
- 반대쪽이 역전파
계산 그래프에서 미분의 효율적 계산
- 오른쪽에서 왼쪽으로 미분값 전달.
왜 한번에 전체 미분을 하지 않고 단계 별로 나누어 미분?
- 복잡한 식에서 연쇄법칙이 더 적은 연산량으로 미분 가능한 방법
- 오차 역전파는 순전파에서 저장한 중간 결과를 재사용 가능 -> 연산량 저감, 빠름
합성 함수
- 여러 함수로 구성된 함수


x에 대해 z를 미분 시..
합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있음
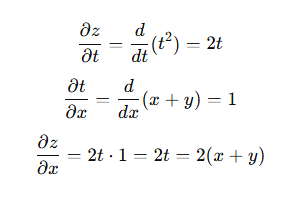
위 합성 함수의 미분은 이처럼 연쇄법칙으로 계산 가능
덧셈 노드의 역전파
- (1을 곱하기만 할 뿐) 입력된 값을 그대로 다음 노드로 보냄
곱셈 노드의 역전파
- 순전파 때의 입력 신호들을 서로 바꾼 값을 곱해서 하류로 보냄
- 덧셈에서는 순방향 입력 신호값이 필요 없는데 곱셈에선 필요 -> 순전파 입력 신호를 변수에 저장해둠
역전파에서 미분 값의 의미
- 사과 값이 1원 오를 때 최종 금액에 2.2원만큼 영향
- 소비세 1만큼 오를 때 최종 금액에 650원만큼 영향
계층 구현
- 모든 계층은 forward와 backword라는 공통의 메서드를 갖도록 구현
곱셈 계층
class MulLayer:
def __init__(self):
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y # x와 y를 바꾼다
dy = dout * self.x
return dx, dy
덧셈 계층
class AddLayer:
def __init__(self):
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy
활성화 계층 구현하기
ReLU 계층
활성화 함수로 사용
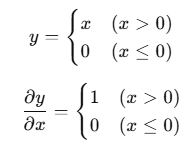
순전파 때 입력 x가 0보다 크면, 역전파는 하류의 값을 그대로 하류로 흘림
순전파 때 x가 0 이하면 역전파 때는 하류로 신호를 보내지 않음
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0) # 0 이하인 값의 위치를 기록
out = x.copy() # 입력을 그대로 복사
out[self.mask] = 0 # 0 이하 위치는 0으로 설정
return out
def backward(self, dout):
dout[self.mask] = 0 # 역전파 시 0 이하였던 위치는 미분값도 0
dx = dout
return dxMask: True, False로 구성된 넘파이 배열
순전파의 입력인 x의 원소값이 0 이하인 인덱스는 True, 그 외는 False로 유지
Sigmoid 계층

y = -x
y = exp(-x)
y = 1 + exp(-x)
y = 1/(1 + exp(-x))
순서로 계산됨
1단계: / 노드에 대한 연산
y = 1/x에 대한 미분
-> dy/dx = -1/x^2 = -y^2
2단계: + 노드는 상류 값을 그대로 하류로
3단계: exp 노드에 대한 연산
y = exp(x)에 대한 미분 => exp(x) => 순전파 때와 같은 출력을 곱해서 내보냄
=> -exp(-x)y^2
4단계: x 노드는 순전파 때의 값을 서로 바꿔 곱
=> exp(-x)y^2
dL/dy(y^2*exp(-x)) = dL/dy( 1 / (1 + exp(-x))^2 ) * exp(-x)
= dL/dy ( 1 / (1 + exp(-x)) ) * ( exp(-x) / (1 + exp(-x)) )
= dL/dy * y(1 - y)
Affine 계층 구현
Y = X*W + B
뉴런의 가중치 합을 위한 행렬 곱: 기하학에서 Affine 변환이라 부름

배치용 Affine 계층의 역전파
순전파의 편향 B는 각 샘플마다 같은 값이 더해짐 (배치 전체에 브로드캐스팅해서 모든 샘플에 같은 값이 더해짐)
X_dot_W = [[10, 10, 10],
[20, 20, 20]] # (2, 3)
B = [1, 2, 3] # (3,)
Y = X_dot_W + B # (2, 3)
Y[0] = [10, 10, 10] + [1, 2, 3] = [11, 12, 13]
Y[1] = [20, 20, 20] + [1, 2, 3] = [21, 22, 23]이렇게 됨

역전파 시에는 모든 데이터에 대한 미분을 더해서 구함

이렇게 되어 있으면

이렇게 구한다는 뜻
Softmax-with-loss 계층
- Softmax + 교차 엔트로피 오차
- 둘을 합치면 역전파 결과가 매우 단순.. 출력 확률에서 정답 벡터를 빼면 끝
- yk - tk
- 우연이 아니고 설계된 결과
'학부 > 빅데이터마이닝' 카테고리의 다른 글
| 합성곱 신경망 (CNN, Convolutional Neural Network) (0) | 2025.06.08 |
|---|---|
| 신경망 학습 관련 기술들 (0) | 2025.06.08 |
| 신경망 학습 / 수치미분 (0) | 2025.06.08 |
| 신경망 손글씨 분류 (MNIST), 순전파(forward propagation) (0) | 2025.06.08 |
| 신경망 (0) | 2025.06.07 |



