| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Multiplay
- 게임 개발
- stride
- Aegis
- 보안
- animation
- local prediction
- gas
- listen server
- rpc
- linear regression
- gameplay tag
- UI
- 언리얼엔진
- widget
- 유니티
- photon fusion2
- os
- 언리얼 엔진
- gameplay ability system
- gameplay effect
- MAC
- CTF
- C++
- unity
- Replication
- ability task
- attribute
- 게임개발
- Unreal Engine
- Today
- Total
Replicated
문맥 자유 문법과 파스 트리 본문
잘 설계된 문법 -> 소스 프로그램을 정확한 목적 코드로 번역할 때 유용한 구조를 제공
좌단유도(leftmost derication), 우단유도(rightmost derivation)
- 좌단유도는 유도 과정의 각 단계에서 문장 형태(sentential form)의 가장 왼쪽에 있는 논터미널 기호를 계속해서 대체하는 경우로 =>_lm으로 표시 (_lm은 => 아래에 쓴다는 뜻)
- 우단유도는 유도 과정의 각 단계에서 문장형태의 가장 오른쪽에 있는 논터미널 기호를 계속해서 대체하는 경우로 =>_rm으로 표시
예. id + (id * id) 유도
P :
E -> E + T | E - T | T
T -> T * F | T / F | F
F -> (E) | id
좌단 유도 풀이
E =>_lm E + T =>_lm T + T =>_lm F + T =>_lm id + T =>_lm id + F
=>_lm id + (E) =>_lm id + (T) =>_lm id + (T * F)
=>_lm id + (F * F) =>_lm id + (id * F) =>_lm id + (id * id)
우단 유도 풀이
E =>_rm E + T =>_rm E + F =>_rm E + (E) =>_rm E + (T)
=>_rm E + (T * F) =>_rm E + (T * id) =>_rm E + (F * id)
=>_rm E + (id * id) =>_rm T + (id * id) =>_rm F + (id * id) =>_rm id + (id * id)
좌파스, 우파스
좌파스(Left parse)
- 하나의 문장을 만들 때 좌단 유도에 의해서 적용된 일련의 생성 규칙 순서
우파스(Right parse)
- 우단 유도를 할 때 적용된 생성 규칙 순서의 역순
예. 좌파스, 우파스 구하기 (id + (id * id), 위에 꺼)
P:
E -> E + T | E - T | T // 각각 1, 2, 3
T -> T * F | T / F | F // 각각 4, 5, 6
F -> (E) | id // 각각 7, 8
좌파스 풀이
E =>_1 E + T =>_3 T + T =>_6 F + T =>_8 id + T =>_6 id + F
=>_7 id + (E) =>_3 id + (T) =>_4 id + (T * F)
=>_6 id + (F * F) =>_8 id + (id * F) =>_8 id + (id * id)
좌파스: 1, 3, 6, 8, 6, 7, 3, 4, 6, 8, 8
우파스 풀이
E =>_1 E + T =>_6 E + F =>_7 E + (E) =>_3 E + (T)
=>_4 E + (T * F) =>_8 E + (T * id) =>_6 E + (F * id)
=>_8 E + (id * id) =>_3 T + (id * id) =>_6 F + (id * id) =>_8 id + (id * id)
우파스는 역순이니
우파스: 8, 6, 3, 8, 6, 8, 4, 3, 7, 6, 1
구문 분석 방법은 크게 두 종류 존재
하향식(top-down) 구문분석: 좌파스 생성
상향식(bottom-up) 구문분석: 우파스 생성
문맥 자유 문법G = (VN, VT, P, S)에 대한 파스 트리(parse tree) 정의
1) 모든 노드의 이름은 문법 기호이다
2) 루트 노드의 이름은 시작기호 S이다
3) 만약 어떤 노드가 하나 이상의 자식을 갖는다면 이 노드의 이름은 논터미널 기호이다
4) 왼쪽부터 순서대로 X1, X2, ... Xn의 n개의 자식을 갖는 어떤 노드 A가 존재한다면 생성규칙 A -> X1X2...Xn이 존재한다
5) 만약 어떤 노드가 자식을 가지고 있지 않다면, 터미널 노드 혹은 리프라 하고 터미널 노드의 이름은 터미널 기호이다
위에 있는 id + (id * id)를 유도하는 파스트리(좌단유도)
E =>_lm E + T =>_lm T + T =>_lm F + T =>_lm id + T =>_lm id + F
=>_lm id + (E) =>_lm id + (T) =>_lm id + (T * F)
=>_lm id + (F * F) =>_lm id + (id * F) =>_lm id + (id * id)
E =>_lm E + T

E + T =>_lm T + T

T + T =>_lm F + T
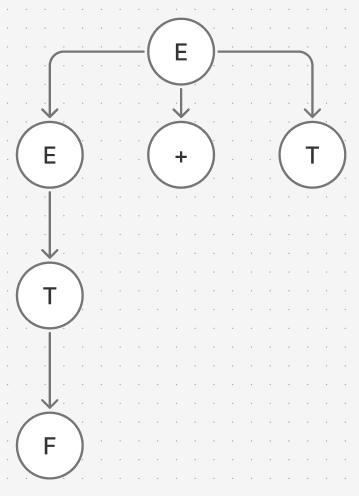
F + T =>_lm id + T

id + T =>_lm id + F

id + F =>_lm id + (E)

id + (E) =>_lm id + (T)

id + (T) =>_lm id + (T * F)

id + (T * F) =>_lm id + (F * F)

(F * F) =>_lm id + (id * F)

id + (id * F) =>_lm id + (id * id)

우단유도라고 다르진 않은데 길어서 스킵
'학부 > 오토마타와 컴파일러' 카테고리의 다른 글
| 문법 변환 : 불필요한 생성 규칙의 제거, ε-생성규칙의 제거 (0) | 2025.11.25 |
|---|---|
| 모호한 문법 (0) | 2025.11.24 |
| 어휘 분석 (0) | 2025.10.12 |
| 정규 언어, 정규 문법, 유한 오토마타의 동치 관계 (0) | 2025.10.12 |
| DFA의 상태수 최소화 (0) | 2025.10.12 |
