| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- local prediction
- linear regression
- photon fusion2
- listen server
- 언리얼 엔진
- Multiplay
- UI
- attribute
- os
- 게임 개발
- unity
- stride
- 보안
- CTF
- 게임개발
- Aegis
- gas
- Replication
- MAC
- ability task
- rpc
- animation
- widget
- gameplay effect
- 유니티
- 언리얼엔진
- C++
- Unreal Engine
- gameplay tag
- gameplay ability system
- Today
- Total
Replicated
정규 언어, 정규 문법, 유한 오토마타의 동치 관계 본문
정규 언어, 정규 문법, 유한 오토마타의 동치 관계
1. 전체 문법이 주어지면 문법으로부터 토큰들을 분리해내고 이 토큰들을 정규 문법으로 표현함
2. 토큰에 대한 정규 문법을 정규 표현으로 표시
3. 정규 언어가 주어지면 정규표현으로 변환하고, 그를 통해 인식기를 만들 수 있다
4. 정규 표현을 인식하는 NFA를 구성, NFA를 DFA로 변환, DFA 최소화 -> 어휘 분석기
정규 문법, 정규 표현, 유한 오토마타는 동치 관계
정규 문법 => 정규 표현
정규 표현 => 유한 오토마타
유한 오토마타 => 정규 문법
정규 문법 => 정규 표현으로 변환
정규 표현에 의해서 정의된 문법 G에 의해 생성되는 언어 L(G)가 무엇인지 알기 위해서,
정규 문법을 정규 표현으로 변환
- 정규 문법을 계수(coefficient)가 정규 표현으로 구성된 방정식인 정규 표현 방정식(regular expression equation)으로 바꾸고 정규 표현 방정식에서 해(solution)를 구함
정규 표현 방정식으로부터 해를 구하는 방법
α, β가 정규 표현이고 α가 ε을 포함하지 않는다면 X = αx + β의 유일한 해
-> X = α*β
증명) X = αx + β의 해가 X = α*β
X = αx + β
= α( α*β ) + β
= α*β + β
= ( α* + ε )β
= α*β
정규 문법 -> 정규 표현 알고리즘
입력: G = ( VN, VT, P, S )
단, VN: 논터미널 기호들의 유한 집합, VT: 터미널 기호들의 유한 집합,
P: 생성 규칙들의 집합 (A->tB, A->t 혹은 A->Bt, A->t, 단 t ∈ VT*, A, B ∈ VN), // 정규 문법 조건
S: 논터미널 기호로서 시작 기호
출력: 정규 문법 G가 생성하는 언어 L(G)를 나타내는 정규 표현
방법:
1. 정규 문법으로부터 정규 표현 방정식을 만든다
2. 정규 표현 방정식 중 X = αx + β 형태를 찾아 X = α*β로 변환한다
3. 시작 기호로부터 출발하여 다른 방정식들을 대입한다. 계산 결과에 X = αx + β 형태의 식이 나타난 경우,
X = α*β 대입 시 정의된 정규 문법 G로부터 생성되는 정규 언어 L(G)를 나타내는 정규 표현이 됨
정규 문법 G = ({S, A, B}, {a, b}, P, S)가 다음과 같을 때, G로부터 생성되는 L(G)를 정규 표현으로
S -> aA | bSA -> aS | bBB -> aB | bB | ε
생성 규칙을 정규 표현 방정식으로 변환하면
S = aA + bS
A = aS + bB
B = aB + bB + ε
이때,
B = (a+b)B + ε 이니 X = αx + β 형태의 식
B = (a+b)*ε
= (a+b)*
S = aA + bS
= a(aS + bB) + bS
= aaS + abB + bS
= aaS + ab(a+b)* + bS
= (aa+b)S + ab(a+b)*
X = αx + β 형태의 식이 되었다
S = (aa+b)*ab(a+b)*
이렇게 시작 기호로부터 구해짐
두번째 예제
정규 문법 G = ({S, A, B}, {a, b}, P, S)
S -> aA | bS
A -> aA | bA | b
S = aA + bS
A = aA + bA + b
A = (a+b)A + b
A = (a+b)*b
S = a(a+b)*b + bS
= bS + a(a+b)*b
S = b*a(a+b)*b
L(G) = b*a(a+b)*b
정규 표현 => 유한 오토마타 변환
- 정규 표현의 정의에 있는 각각을 받아들이는 ε-NFA를 구성
- 정규 표현 ø, ε, a

정규 표현 N1+N2, N1·N2, N*에 대해
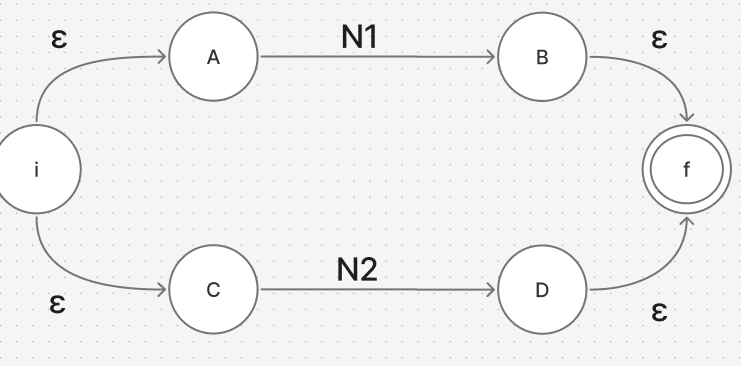
N1+N2

N1·N2
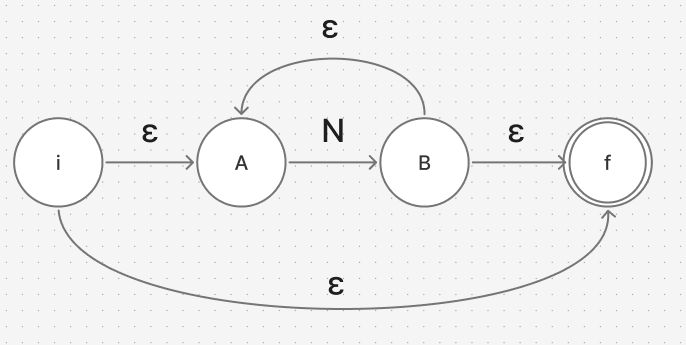
N*
정규 표현 (a+b)*를 인식하는 유한 오토마타 구성

a를 인식하는 유한 오토마타, b를 인식하는 유한 오토마타
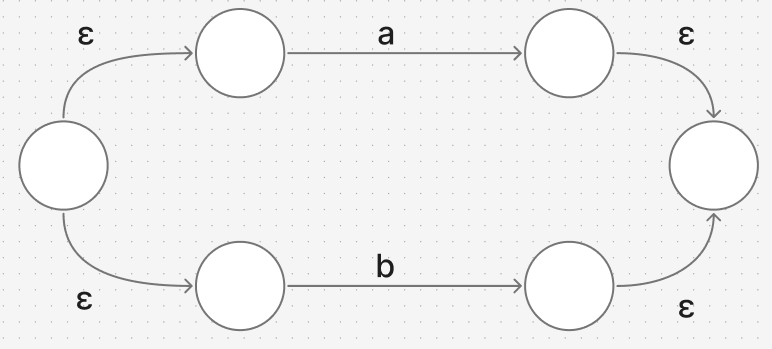
a+b를 인식하는 유한 오토마타

(a+b)*를 인식하는 유한 오토마타
추가로
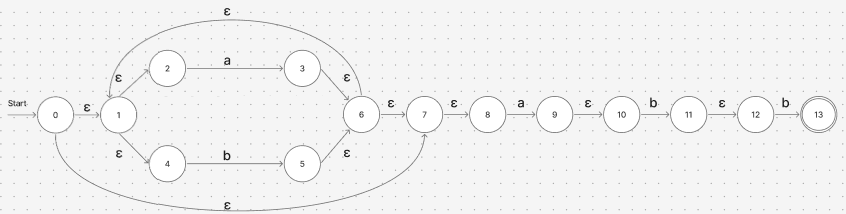
(a+b)*abb
유한 오토마타를 정규 문법으로 변환
유한 오토마타 M =(Q, Σ, δ, q0, F) 로부터 정규 문법 G = (VN, VT, P, S) 만들기
입력: 유한 오토마타 M =(Q, Σ, δ, q0, F)
단, Q : 상태들의 유한 집합
Σ : 입력 기호들의 유한 집합
δ : 상태 전이 함수
q0: 종결 기호
출력: 정규문법 G = (VN, VT, P, S)
단, VN : 논터미널 기호들의 집합
VT : 터미널 기호들의 집합
P : 생성 규칙의 집합
S : 시작 기호
방법:
VN = Q
VT = Σ
S = q0
P :
if δ(q, a) = r, then q -> ar;
if q ∈ F, then q -> ε;
예시

이 유한 오토마타를 정규 문법으로 바꿔보자
G = (VN, VT, P, S)
단, VN = {A, B, C, D}
VT = {a, b}
S = A
P :
A -> aA | bA | aB
B -> bC
C -> bD
D -> ε
정규 언어, 정규 문법, 유한 오토마타는 서로 변환도 되는 동치 관계이다
(정규 언어는 정규 표현으로 표현됨)
'학부 > 오토마타와 컴파일러' 카테고리의 다른 글
| 문맥 자유 문법과 파스 트리 (0) | 2025.11.23 |
|---|---|
| 어휘 분석 (0) | 2025.10.12 |
| DFA의 상태수 최소화 (0) | 2025.10.12 |
| NFA의 DFA 변환 및 ε-전이 (0) | 2025.10.11 |
| 결정적 유한 오토마타(DFA), 비결정적 유한 오토마타(NFA) (0) | 2025.10.11 |

