| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 유니티
- MAC
- animation
- 언리얼엔진
- Replication
- rpc
- widget
- gameplay tag
- stride
- os
- gas
- 게임개발
- 언리얼 엔진
- unity
- UI
- Unreal Engine
- Aegis
- Multiplay
- gameplay effect
- linear regression
- listen server
- CTF
- gameplay ability system
- attribute
- photon fusion2
- 게임 개발
- 보안
- ability task
- C++
- local prediction
Archives
- Today
- Total
Replicated
DTFT & properties, Convolution 본문
Discrete-Time Fourier Transform
DTFT => 아날로그 시그널은 descrete signal로 변환 (Frequency Spectrum)
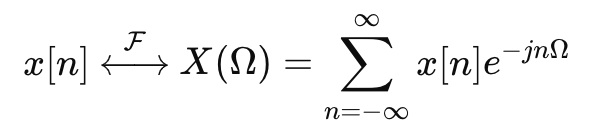
Frequency Spectrum : |X(Ω)|
DTFT가 존재하려면? ..
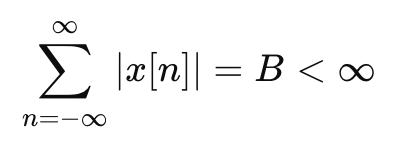
만족해야 함
문제
오메가는 라디안 프리퀀시 .. 연속적임
=> DFT 사용
하지만 얘는 느림
=> FFT 사용
FFT (Fast Fourier Transform)
- 1965, Cooley와 Turkey
- DSP 시스템이 실시간에 작동하도록 만들어줌
ex.
x[n] = δ[n]
=> DTFT 취하면 X(Ω) = 1 .. 모든 주파수 대역에 영향을 끼침
=> White noise .. 반대를 color noise라 함
x[n] = δ[n-n0] => e^-njΩ
x[n] = {1, 0, 3, 2} => 1 + 3e^-j2Ω -2e^j3Ω
x[n] = a^nu[n] => 1/(1-ae^-jΩ)
DTFT Properties
- Periodity
2𝜋 주기성을 가짐
- Euler's identity
e^-jnΩ = cos(nΩ) - jsin(nΩ) = ( cos(Ω) - jsin(Ω) )^n
- Linerity
ax1[n] + bx2[n] <=> aX1(Ω) + bX2(Ω)
- Shifting property
x[n-n0] <=> e^-jnΩX(Ω)
- Time-reversal
x[-n] <=> x(-Ω)
Convolution
y[n] = x[n]*h[n]
<=>
Y(Ω) = X(Ω) x H(Ω)
'학부 > 멀티미디어신호처리' 카테고리의 다른 글
| DFT (Discrete Fourier Transform) (0) | 2024.12.02 |
|---|---|
| Frequency response (0) | 2024.12.01 |
| Discrete Cross-Correlation (0) | 2024.11.30 |
| Convolution (0) | 2024.11.30 |
| Moving Average Filter, Echo, Reverberation (0) | 2024.11.30 |




