| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- stride
- 보안
- 언리얼엔진
- 유니티
- gameplay tag
- photon fusion2
- 게임개발
- gas
- Aegis
- local prediction
- 언리얼 엔진
- gameplay ability system
- level design
- animation
- Replication
- CTF
- ability task
- widget
- 게임 개발
- attribute
- UI
- os
- rpc
- gameplay effect
- unity
- C++
- Unreal Engine
- MAC
- listen server
- Multiplay
- Today
- Total
Replicated
Frequency response 본문
H(Ω) = Y(Ω) / X(Ω)
프리퀀시 리스폰스는 시스템의 특성을 나타냄
구하는 방법
1. 선형 차분 방정식 나눠서(Y(Ω) / X(Ω)) 구하기
2. 임펄스 리스폰스에 DTFT 취하기
H(Ω) = HR(Ω) + jHI(Ω)
위의 프리퀀시 리스폰스는 컴플렉스 폼.. (Rectangular form)
H(Ω) = |H(Ω)|e^jθ(Ω)
** θ(Ω) = arctan(HI(Ω)/HR(Ω))

페이즈 리스폰스보다는 매그니튜드 리스폰스가 중요
20log|𝐻(Ω)| v.s. Ω
로그는 결과 0 이하 값 ( 입력 1이하 ) 을 굉장히 자세히 보여줌
스탑 밴드의 성능을 보기 위해 사용
Magnitude Spectrum
2파이를 주기로 주기적인 특성이 있음
그리고 좌우 대칭 구조를 보임 (even function .. impulse response기 real function이면 DTFT는 항상 even func)
=> 0~파이 구간만 계산하면 됨
Comb Filter
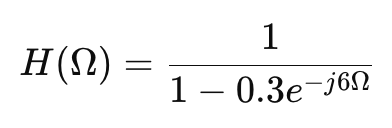

이걸 그리면 빗같이 생기게 나옴 => comb filter
time domain에서 reverberation으로 나타남
Digital radian frequency & analog freqency
우리는 평소에 파이 기준으로 말하지 않고 Hz 기준으로 말함 => 변환 필요

F: digital frequncy
f: analog frequency
fs : sampling rate
0 <= Ω <= 𝜋 <-> 0 <= f <= fs/2
예를 들어 fs가 12kHz이면, Magnitude spectrum은 6kHz까지 나타남
'멀티미디어신호처리' 카테고리의 다른 글
| FFT, Redix-2 DIT FFT (0) | 2024.12.07 |
|---|---|
| DFT (Discrete Fourier Transform) (0) | 2024.12.02 |
| DTFT & properties, Convolution (0) | 2024.12.01 |
| Discrete Cross-Correlation (0) | 2024.11.30 |
| Convolution (0) | 2024.11.30 |




