| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- unity
- widget
- 게임개발
- attribute
- gameplay ability system
- animation
- gameplay effect
- local prediction
- Unreal Engine
- Multiplay
- 언리얼엔진
- stride
- photon fusion2
- UI
- 보안
- MAC
- rpc
- Aegis
- CTF
- level design
- gas
- ability task
- Replication
- 언리얼 엔진
- 유니티
- gameplay tag
- listen server
- os
- 게임 개발
- C++
- Today
- Total
Replicated
FFT, Redix-2 DIT FFT 본문
실시간으로 연산 가능할 정도로 DFT를 빠르게 계산하는 알고리wma
Radix-2 decimation -in-time (DIT) FFT
- N 포인트로 근사되어 있다고 할 때,
2 ~ N/2 포인트 -> 4 ~ N/4포인트 .. 쪼개서 2포인트 되게 하고 계산 => Radix-2 DIT(decimation-in-time) FFT

DFT식이 위와 같을 때 ..
x[2m] = {x[0], x[2], x[4], .... x[N - 2]}
x[2m + 1] = {x[1], x[3], x[5], ... x[N - 1]}

이렇게 분할 가능

정리 시 위와 같음
Y[k]는 홀수 부분 DFT, Z[k]는 짝수 부분 DFT
* Twiddle factor
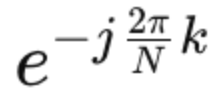
...
Y[k]가 N/2 포인트 DFT일 때, 주기는 N/2임
Y[k + N/2] = Y[k] .. Z[k]도 마찬가지
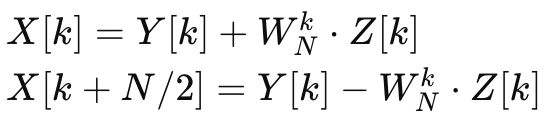
Wnk가 Twiddle Factor일 때,
이렇게 나타남
-가 붙은 이유는 유닛 서클을 생각하면 됨 (e^(-jπ)가 -1이니 -가 곱해짐
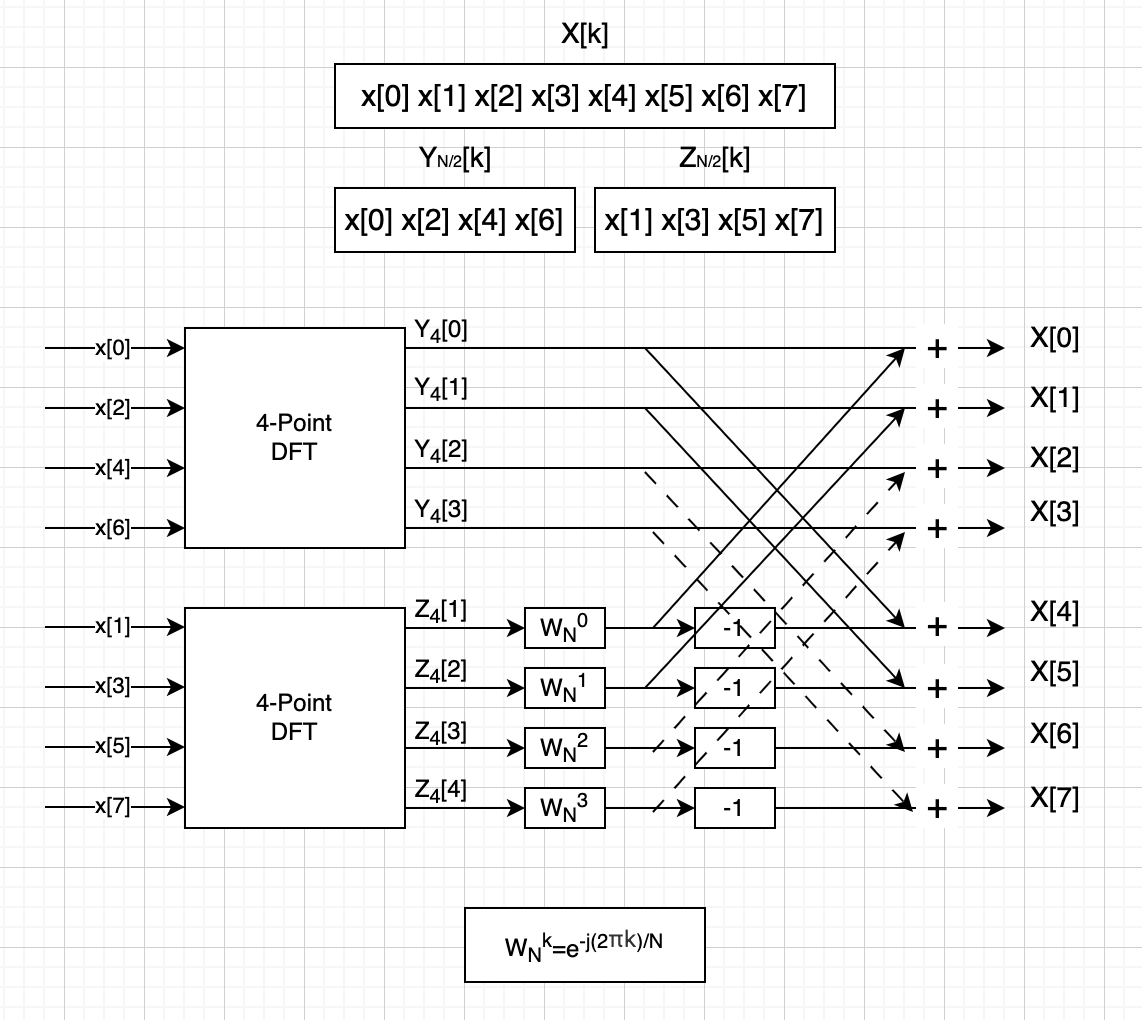
위는 n이 4로만 쪼개는데 실제로는 2개만 남을 때까지 쪼개야 함

그럼 이 계산에서 인풋 시퀀스를 어떻게 알고 줄 것이냐 ..
=> bit reversing
| n | Binary | Bit-reversed binary | n |
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
시간복잡도: NlgN
Fast convolution using FFT
y[n] = x[n]*h[n] <-> Y(k) = X(k)H(k)
-> y[n] = IFFT{Y(k)}
y[n] = IFFT{ FFT{x[n]}FFT{h[n]} }
x랑 h의 길이가 다르면 이걸 어떻게 하는가
=> 엔딩 포인트는 N + M - 2이고, 길이는 N + M - 1
맞춰서 zero padding
ex. FFT convolution
x[n] = {2, 5, 0, 4}
h[h] = {4, 1, 3}
엔딩 포인트 : 4 + 3 - 1 = 6 < 2^3 = 8
x[n] = {2, 5, 0, 4, 0, 0, 0, 0}
h[h] = {4, 1, 3, 0, 0, 0, 0, 0}
이걸 각각 FFT 취하고, 곱하고, 인버스 FFT 취하면 y[n] 나옴
'멀티미디어신호처리' 카테고리의 다른 글
| Magnitude response & Phase response (0) | 2024.12.07 |
|---|---|
| Euler's Formula & Identity (0) | 2024.12.07 |
| DFT (Discrete Fourier Transform) (0) | 2024.12.02 |
| Frequency response (0) | 2024.12.01 |
| DTFT & properties, Convolution (0) | 2024.12.01 |




