| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- gameplay effect
- UI
- Aegis
- os
- 언리얼엔진
- CTF
- Multiplay
- Replication
- 게임 개발
- gas
- attribute
- stride
- unity
- 언리얼 엔진
- 보안
- 게임개발
- local prediction
- MAC
- gameplay ability system
- C++
- ability task
- rpc
- photon fusion2
- animation
- linear regression
- Unreal Engine
- gameplay tag
- widget
- listen server
- 유니티
- Today
- Total
Replicated
로지스틱 회귀 본문
분류 문제: 몇 가지 이산적 값 중 하나를 선택하는 모델 == 분류 모델
일반 선형 회귀처럼 선 하나 쭉 그어넣고 위는 0, 아래는 1 이렇게 못함
로지스틱 회귀의 개념
- 이진 분류(binary classification) 문제를 확률로 표현
- 어떤 확률이 일어날 확률 P(X), 일어나지 않을 확률 1 - P(X) .. (0 <= P(X) <= 1)
- 오즈비(odds ratio) : 어떤 사건이 일어날 확률과 일어나지 않을 확률의 비율, P(X) / (1 - P(X))
.. 수식 상 확률이 올라갈수록 => 오즈비 급상승
로짓(logit) 함수 : 오즈비에 상용로그 붙인 수식

x가 들어왔을 때 y가 1일 확률(성공) => 그냥 P(X)라 보면 됨

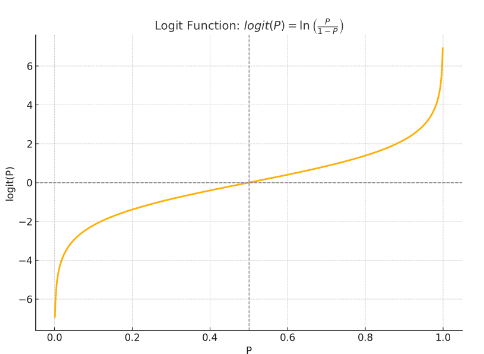
로짓 함수와 Logistic(Sigmoid)함수는 역함수 관계 (y=x에 대해 대칭)



이렇게 변형되고

결과
로지스틱 함수(logistic function) : 로짓 함수의 역함수

- 그래프가 S자 커브 형태인 시그모이드 함수
- 종속 변수가 이분형일 때 수행할 수 있는 예측 분석을 위한 회귀분석
- 0과 1 사이.. 확률 예측에 적합
가설함수

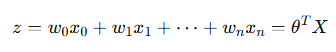
- z는 가중치 값과 피쳐 값의 선형 결합
- 가중치 값을 찾는 학습을 위해 경사하강법 알고리즘 사용
비용함수

0 <= h <= 1
실제값이 1, 0일 때 각각 다르게 비용함수 정의
y=1이면 가설함수 값이 커질수록 비용함수 감소, y=0이면 가설함수 값이 작아질 수록 비용함수 증가

y가 1이면 오른쪽이 사라지고 0이면 왼쪽이 사라짐
비용 함수의 미분과 가중치 업데이트
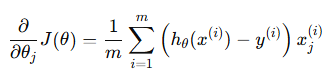

'학부 > 빅데이터마이닝' 카테고리의 다른 글
| 로지스틱 회귀 구현 (0) | 2025.04.12 |
|---|---|
| 분류 문제의 성능 지표 (0) | 2025.04.12 |
| 과대적합과 정규화 (0) | 2025.04.11 |
| 경사하강법 실습 (0) | 2025.04.08 |
| 경사하강법의 종류 (0) | 2025.04.07 |




