| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- stride
- gameplay tag
- ability task
- gas
- photon fusion2
- gameplay ability system
- listen server
- 게임개발
- os
- animation
- CTF
- 유니티
- unity
- Multiplay
- Aegis
- widget
- local prediction
- 언리얼 엔진
- gameplay effect
- MAC
- attribute
- Unreal Engine
- C++
- rpc
- Replication
- 게임 개발
- UI
- linear regression
- 보안
- 언리얼엔진
- Today
- Total
Replicated
베이즈 분류기 본문
이산형 값의 확률
- P(X) = count(Event.x) / count(Event.allevent)
연속형 값의 확률
- 적분
확률의 기본 성질
- 확률은 모든 사건에 대해 반드시 0~1 사이에 값을 가짐, 0 <= P(X) <= 1
- 각 사건들이 서로 관계가 없는 경우, 즉 각 사건이 일어날 확률이 다른 사건이 일어날 확률에 영향을 미치지 않을 때 각 사건들이 독립되었다고 정의
조건부 확률(conditional probability)
- 어떤 사건이 일어난다고 가정했을 때 다른 사건이 일어날 확률
- P(A|B) : B 발생했을 때 A와 B 사건의 교집합이 발생할 확률
P(A | B) = P(A ∩ B) / P(B)
A = {x | x는 홀수}, B = {x | x는 4 이하의 수}
=> P(A | B) = 1/2
베이즈 정리(Bayes's theorem)
- 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리
- 전제: 객관적인 확률이 존재하지 않고 이전 사건으로 인해 확률이 지속적으로 업데이트됨
H는 가설, D는 데이터일 때
P(H|D) = P(H)P(D|H) / P(D)
- P(H|D) : 사후확률(posterior) - 데이터 D가 주어졌을 때 해당 가설 H가 맞을 확률
- P(H) : 사전확률(prior) - 데이터가 없을 때 가설 H가 맞을 확률
- P(D|H) : 가능도(likelihood) - 가설 H가 맞을 때 데이터 D가 발생할 확률
- P(D) : 데이터 D가 발생할 확률
베이즈 분류기
- 메일에 비아그라(viagra)라는 단어가 들어가면 어느 정도의 확률로 스팸메일인지 판단
P(span|viagra) = P(spam)P(viagra|spam) / P(viagra)
| number | viagra | spam |
| 1 | 1 | 1 |
| 2 | 0 | 0 |
| 3 | 0 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 0 | 0 |
| 7 | 0 | 1 |
| 8 | 0 | 1 |
| 9 | 1 | 1 |
| 10 | 1 | 0 |
| 11 | 1 | 0 |
| 12 | 0 | 0 |
| 13 | 0 | 0 |
| 14 | 1 | 0 |
| 15 | 0 | 0 |
| 16 | 0 | 0 |
| 17 | 0 | 0 |
| 18 | 0 | 1 |
| 19 | 0 | 1 |
| 20 | 1 | 1 |
P(spam|viagra) = 6/20 * 3/6 / 6/20 = 1/2
베이즈 분류기 구현
from pandas import Series, DataFrame
import pandas as pd
import numpy as np
viagra_spam = { 'viagra':
[1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1],
'spam':
[1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1]}
df = pd.DataFrame(viagra_spam, columns = ['viagra', 'spam'])
np_data = df.values
np_data.shape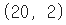

P(viagra), P(spam), P(spam ∩ viagra), P(spam ∩ ~viagra)

P(spam | viagra), P(spam | ~viagra)
viagra라는 단어가 포함되었을 때 스팸메일일 확률은 아닐때보다 확률이 높음
근데 viagra라는 단어 외에 영향을 주는 단어가 있을 수 있고, 오히려 스팸에서 제외되는 메일에 viagra가 존재하고 있을 가능성도 있음
-> 나이브 베이지안 분류기가 위 문제점을 해결
'학부 > 빅데이터마이닝' 카테고리의 다른 글
| 퍼셉트론 (Perceptron) (0) | 2025.06.07 |
|---|---|
| 나이브 베이지안 분류기 (0) | 2025.04.12 |
| 다중클래스 분류의 코드 구현 (0) | 2025.04.12 |
| 다중클래스 분류 & 소프트맥스 분류 (0) | 2025.04.12 |
| 로지스틱 회귀 구현 (0) | 2025.04.12 |



